无模型的深度强化学习算法已经在一系列的决策和控制任务上得到了证明。但是,这些方法通常面临两大挑战:非常高的样本复杂性和脆弱的收敛特性,这需要精心的超参数调整。这两个挑战严重限制了这些方法在复杂、真实世界领域的应用性。(训练非常不稳定,收敛性较差,对超参数比较敏感,也难以适应不同的复杂环境。)
在本文中,我们提出了基于最大熵强化学习框架的Soft Actor-Critic(SAC)的离线策略算法。在这个框架中,Actor 旨在最大化预期奖励,同时也最大化熵。也就是说,在尽可能随机的行动下成功完成任务。SAC 的前身是 Soft Q-learning,它们都属于最大熵强化学习的范畴。Soft Q-learning 不存在一个显式的策略函数,而是使用一个函数Q的波尔兹曼分布,在连续空间下求解非常麻烦。目前,在无模型的强化学习算法中,SAC 是一个非常高效的算法,它学习一个随机性策略,在不少标准环境中取得了领先的成绩。1
最大熵强化学习
SAC的一个核心特征是熵正则化。策略被训练成在预期回报和熵之间找到一个权衡,其中熵是策略中的随机性度量。这与exploration-exploitation的权衡有密切关系:增加熵会导致更多的exploration,从而可以加速后续的学习。它还可以防止策略过早地收敛到不良的局部最优解。
熵(entropy)表示对一个随机变量的随机程度的度量。具体而言,如果 X 是一个随机变量,且它的概率密度函数为 p,那么它的熵 H 就被定义为
在强化学习中,我们可以使用来表示策略 π 在状态 s 下的随机程度。
最大熵强化学习(maximum entropy RL)的思想就是除了要最大化累积奖励,还要使得策略更加随机。如此,强化学习的目标中就加入了一项熵的正则项,agent 在每个时间步获得与该时间步的策略熵成比例的reward[^SAC - Spinningup]:
其中,α 是一个正则化的系数,用来控制熵的重要程度。SAC 算法学习的目标是最大化熵正则化的累积奖励而不只是累计奖励, 从而鼓励更多的探索。
熵正则化增加了强化学习算法的探索程度,α 越大,探索性就越强,有助于加速后续的策略学习,并减少策略陷入较差的局部最优的可能性。
Soft 策略迭代
在最大熵强化学习框架中,由于目标函数发生了变化,其他的一些定义也有相应的变化。
令
则有 Soft Bellmen equation:
其中,状态价值函数被写为( 和 被联系起来了):
于是,根据该 Soft 贝尔曼方程,在有限的状态和动作空间情况下,Soft 策略评估可以收敛到策略 π 的 Soft Q函数。然后,根据如下 Soft 策略提升公式可以改进策略:
SAC
在 SAC 算法中,我们为两个动作价值函数 (参数分别为和) 和一个策略函数 (参数为)建模。基于 Double DQN 的思想,SAC 使用两个网络,但每次用网络时会挑选一个值小的网络,从而缓解值过高估计的问题。SAC使用一个最小化Q值的目标Q网络来生成一个保守的、悲观估计,以确保 agent 不会高估Q值。这在训练中非常有用,因为高估Q值可能导致代理做出不稳定的、不可靠的决策,甚至可能导致不良策略。这有助于提高训练的稳定性和鲁棒性,使得代理更容易学习到高质量的策略。
任意一个网络的损失函数为:
其中,就是td_target,r 是策略过去收集的数据,因为 SAC 是一种离线策略算法:
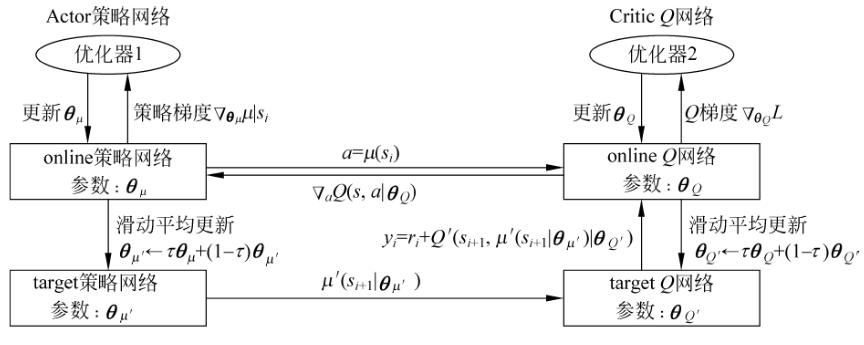
SAC 中目标网络的更新方式与DDPG 中的更新方式相似。
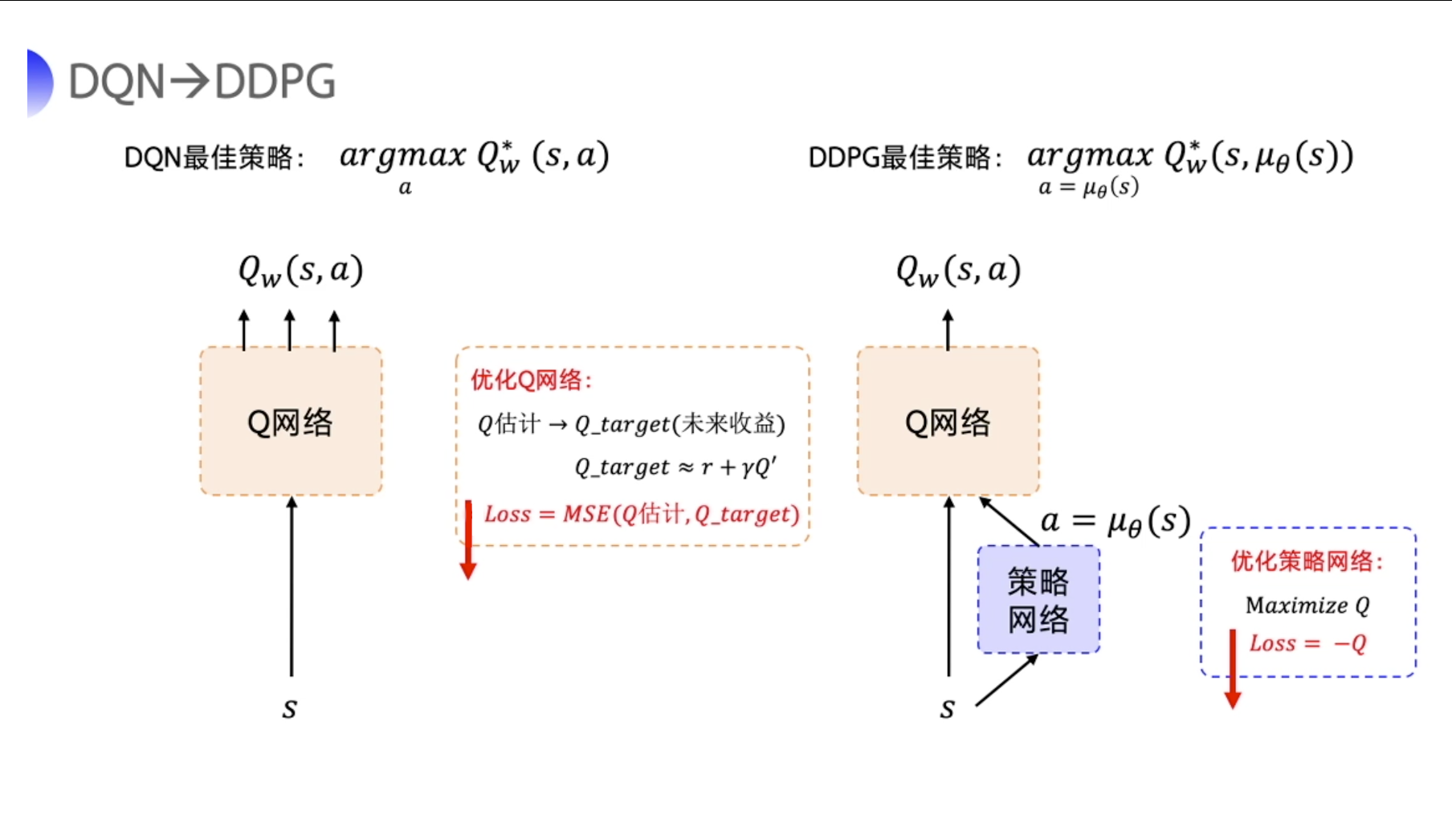
REINFORCE 算法每隔一个 episode 就更新一次,但 DDPG 网络是每个 step 都会更新一次 policy 网络,也就是说它是一个单步更新的 policy 网络。DDPG 直接在 DQN 基础上加了一个策略网络来直接输出动作值,所以 DDPG 需要一边学习 Q 网络,一边学习策略网络。2不过,SAC 优化策略网络的方式略有差异。
SAC算法有两套Q网络,这点与DDPG相似。引入目标网络是为了更好的计算td_target。目标网络中的参数是通过软更新的方式来缓慢更新的,因此它的输出会更加稳定,利用目标网络来计算目标值自然也会更加稳定,从而进一步保证Critic网络的学习过程更加平稳。3如果使用同一张神经网络来表示目标网络(target network)和当前更新网络(online),学习过程会很不稳定。因为同一个网络参数在频繁地进行梯度更新的同时,还需要被用于计算网络的梯度。4
Deep Deterministic Policy Gradient(DDPG)的中文含义为:深度确定性策略梯度。确定性策略,确定性策略虽然在同一个状态处,采用的动作概率不同,但采取的是最大概率的那一个。作为确定性策略,相同的策略,在同一个状态处,动作是唯一确定的,。SAC在这点上与之不同,SAC采用的是随机策略。
策略的损失函数由 KL 散度得到,化简后为:
可以理解为最大化函数,因为有,正好为其负值。对连续动作空间的环境,SAC 算法的策略输出高斯分布的均值和标准差,但是根据高斯分布来采样动作的过程是不可导的。因此,我们需要用到重参数化技巧 (reparameterization trick)。 **重参数化的做法是先从一个单位高斯分布采样,再把采样值乘以标准差后加上均值。这样就可以认为是从策略高斯分布采样,并且这样对于策略函数是可导的。**也可以减少梯度估计的方差。重参数化的做法将 表示成一个使用状态 s 和标准正态样本 ϵ 作为其输入的函数直接输出动作 a,我们将其表示为,是一个噪声随机变量。2
因为有两个网络,重写策略的损失函数:
在 SAC 算法中,如何选择熵正则项的系数非常重要。在不同的状态下需要不同大小的熵: 在最优动作不确定的某个状态下,熵的取值应该大一点; 而在某个最优动作比较确定的状态下,熵的取值可以小一点。为了自动调整熵正则项,SAC 将强化学习的目标改写为一个带约束的优化问题:
也就是最大化期望回报,同时约束熵的均值大于。通过一些数学技巧化简后,得到α的损失函数:
即当策略的熵低于目标值时,训练目标会使的值增大,进而在上述最小化损失函数 的过程中增加了策略熵对应项的重要性; 而当策略的熵高于目标值时,训练目标会使的值减小,进而使得策略训练时更专注于价值提升。
算法流程:

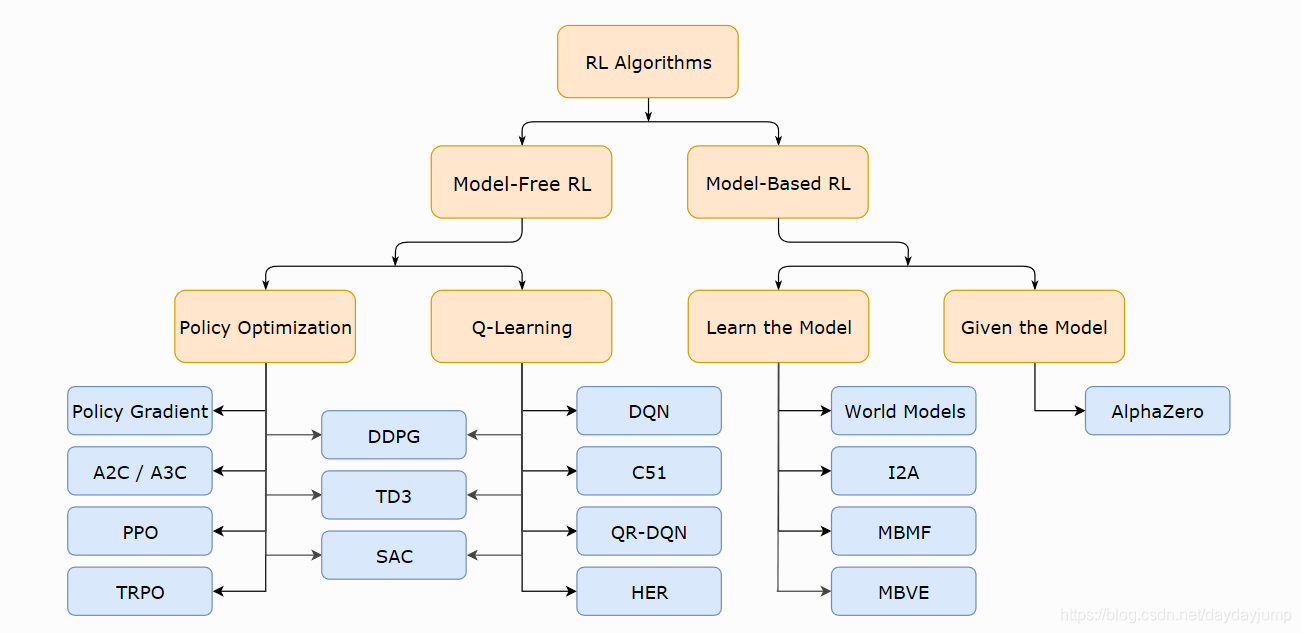
Footnotes
-
https://hrl.boyuai.com/chapter/2/sac%E7%AE%97%E6%B3%95 [^Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor]: https://arxiv.org/abs/1801.01290 [^SAC - Spinningup]: https://spinningup.openai.com/en/latest/algorithms/sac.html ↩
-
https://blog.csdn.net/weixin_42301220/article/details/123375055 ↩ ↩2
-
https://blog.csdn.net/weixin_46133643/article/details/124356983 ↩
-
https://blog.csdn.net/qq_42192693/article/details/123830097 ↩
